Pour ce cours nous allons continuer à expliquer les règles mathématiques de bases en algèbre Booléenne, pour ensuite comprendre comment avec les transistor nous pouvons faire de la logique.
Les propriétés mathématiques de l’algèbres de Boole sont très importantes pour pouvoir construire facilement des portes logiques sur demande. Tout les opérations mathématiques « classique » de base comme l’addition, la soustraction, la multiplication sont décrites par cette logique composée que de $0$, $1$ ou FAUX, VRAI. Si on compose correctement les portes logiques on peut obtenir un ensemble capable de calculer et voire faire des algorithmes. Le but est donc de comprendre les différentes propriétés avec les opérateur $+$ et $\cdot$.
En deuxième partie, le transistor sera à l’honneur. Un transistor est un composant électronique qui permet de faire des portes logique si combiné de manière habile. Cette partie sera un peu plus physique et électronique que le reste du cours.
1. Propriétés des opérateurs logiques :
Soit a, b et c une entrée logique qui peut prendre comme valeur $0$ ou $1$ (FAUX ou VRAI),
Associativité
On defini l’associativité comme avec l’addition, pour l’opérateur OU : $(a + b) + c = a + (b + c) = a + b + c$.
Pour l’opérateur ET : $(a \cdot b) \cdot c = a \cdot (b \cdot c) = a \cdot b \cdot c$.
Cette propriété peut paraitre triviale, mais en réalité elle est très importante, elle permet d’enlever les parenthèses inutiles.
Commutativité
Tout comme la précédente celle-ci n’est pas difficile a comprendre mais a son importance, pour l’opérateur OU : $a + b = b + a$.
Pour l’opérateur ET : $a \cdot b = b \cdot a$
C’est très classique, mais pas toujours vrai avec tout les objets mathématiques comme par exemple les matrices pour lesquelles la commutativité n’est pas vraie sur la multiplication.
Distributivité
La distributivité n’est pas exactement comme pour la multiplication et l’addition puisque on peut distribuer sur $+$ et $\cdot$, pour l’opérateur OU : $a + (b \cdot c) = (a + b) \cdot (a + c)$
Pour l’opérateur ET : $a \cdot (b + c) = (a \cdot b) + (a \cdot c)$.
En réalité il n’y a pas de priorité comme la multiplication sur l’addition, $+$ et $\cdot$ ont la même « importance » d’où le fait que la distributivité agisse sur les deux opérateurs.
Eléments neutres et absorbants
L’élément neutre correspond à l’élément qui ne change pas l’équation, pour OU : $a + 0 = a$
pour ET : $a \cdot 1 = a$.
L’élément absorbant est au contraire un élément qui absorbe l’entrée, pour OU : $a + 1 = 1$
pour ET : $a \cdot 0 = 0$.
Involution
La négation de la négation donne la sortie, $a = \overline{\overline{a}}$.
Tier exclu, contradiction et idempotence
$a + \overline{a} = 1$, $a \cdot \overline{a} = 0$ et $a + a = a$, $a \cdot a = a$.
Avec toutes ces propriétés nous sommes capable de faire des calculs logiques. Par exemple il devient très facile de simplifier des calculs. L’équation suivant peut se simplifier, $$a \cdot (\overline{a} + b) + (a \cdot \overline{b}) = (a \cdot \overline{a}) + (a \cdot b) + (a \cdot \overline{b}) = 0 + a \cdot (b + \overline{b}) = 0 + a \cdot 1 = a.$$ En effet on part d’une équation plutôt compliquée pour arriver sur juste $a$ ce qui est très pratique pour éviter de rajouter beaucoup trop de portes logiques inutilement.
2. Les transistors :
Fonctionnement
Le transistor est donc un composant électronique qui n’est pas un dipôle classique, mais un semi-conducteur. Il a trois pattes et sert comme interrupteur : soit allumé et le courant passe, soit éteint le courant ne passe pas ($0$, $1$). C’est donc le parfait composant qui traduit de manière automatique le langage logique en circuit électronique. Dans la plupart des processeur on utilise des transistor MOS qui sont dotés d’un Drain (D), d’une Source (S) et d’une Grille (G).
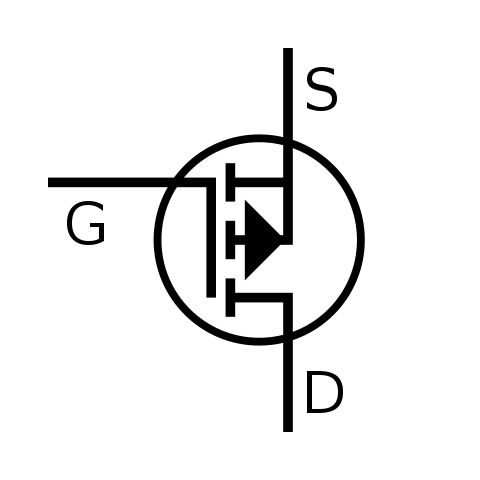
Ce composant est très particulier car il permet de contrôler le courant qui passe de S => D grâce à la tension entre G et S. Si la tension $V_\mathrm{GS}$ est supérieur a un seuil $V_\mathrm{TH}$ alors le courant passe entre S et D, sinon le courant ne passe pas. Il suffit donc de designer l’état haut $1$ tel que $V_\mathrm{GS} > V_\mathrm{TH}$ et l’état bas $0$ tel que $V_\mathrm{GS} < V_\mathrm{TH}$. Nous pouvons simplifier les schéma des transistors par ce schéma, ou $a$ représente un entrée logique ($0$, $1$)
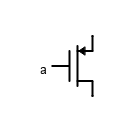
Notre première porte logique
Nous pouvons donc faire notre première porte logique, qui sera juste passant tel que,
| $a$ | $S$ |
| $0$ | $0$ |
| $1$ | $1$ |
Il faut donc mettre un transistor et mettre l’entrée $a$ sur la grille et la sortie $S$ sur le drain, de telle manière que $S = a$. Il existe une subtilité, l’état haut prévaut sur l’état bas, c’est à dire que si un câble relie un état haut et un état bas alors c’est l’état haut qui se propage dans le câble. De plus il faut savoir qu’il faut absolument forcer un état, car il peut être indéterminé, il faut toujours le connecter à un état haut ou bas. Ici si je met ce transistor comme ceci alors si on allume $a$ (en mettant une tension supérieure à la tension seuille) alors l’état haut sort dans $S$ (car le transistor est passant), sinon on force l’état bas quand $a = 0$.
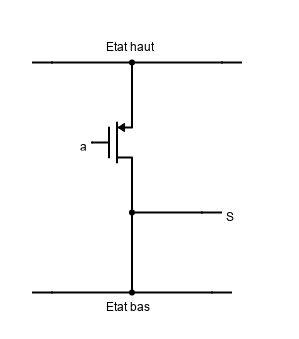
La porte logique passante est donc faite mais elle n’a pas énormément d’intérêt. Avec ces deux parties nous pouvons de mieux en mieux comprendre comment est fait un processeur, en réalité ce sont des transistors qui agissent comme interrupteurs automatiques. Grâce à la logique nous pourrons très prochainement faire des opération sur les bits et donc par exemple les additions. Mais pour ça il faut fabriquer toutes les portes logiques qui seront explicitées dans le prochain cours.


