Ce cours sera exclusivement porté sur la création de la porte logique ET. C’est a partir de cette porte logique que beaucoup de choses sont accomplies en électronique.
Cette porte permet de laisser passer le courant que quand deux entrées (voire plus) sont allumées en même temps. Par exemple vous avez deux interrupteur connecté à une porte ET, la lampe s’allumera que si les deux interrupteurs sont en position fermé. La porte ET sera plus connue sous le nom AND (logic gate AND). L’opération est élémentaire et permet avec l’opération OU de faire toute les autres portes logiques. Comme vu au cours précédent l’équation caractérisée par la porte ET est : soit $a$ et $b$ deux entrées booléennes alors $S_{\mathrm{ET}} = a \cdot b$ et a pour table de vérité :
| $a$ | $b$ | $S$ |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
1. Comment obtenir une porte logique ET :
La porte logique ET doit donc être câblée avec des transistors tout comme la porte logique passante du cours précédent. Cette fois ci il y a deux entrées donc, on peut facilement se dire qu’il faut deux transistors : et ceci est totalement vrai. Mais maintenant comment les agencer ? Il faut forcer un état haut que quand les deux transistors sont passants. On peut voir ça comme si le premier transistor amène l’état haut vers le deuxième, qui lui choisi si l’état haut passe ou pas. Mais si l’état n’est pas haut pour le premier transistor alors il ne peut y avoir d’état haut dans le deuxième (car il est apporté par le premier transistor). L’une des solutions est donc de mettre les transistors en séries, comme ceci :
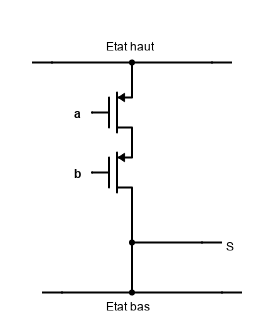
Ici si les deux transistors sont passant alors la sortie sera à l’état haut, sinon la sortie est forcé à l’état bas. Comme vu au cours précédent l’état haut prévaut sur le bas. Cette porte logique a donc un schéma qui lui est approprié :
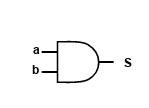
Ici on remarque un petite subtilité, les état haut et bas sont omis. Cela est tout à fait normal, dans les schémas de porte logique et d’assemblages de portes logiques en réalité les hauts et bas ne sont plus représenté par soucis de lisibilité.
2. Assembler des portes ET, pour faire des portes ET à $n$ entrées :
Maintenant, nous cherchons à faire des portes logiques ET à $n$ entrées qui respectent donc l’équation suivante : $S = a_0 \cdot a_1 \cdot a_2 … \cdot a_n$. Pour ce faire nous allons observer comment faire une porte logique ET à trois entrées, qui a pour table de vérité :
| $a_0$ | $a_1$ | $a_2$ | S |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Comme le suggère l’équation (si on rajoute des parenthèses au bon endroit) $S = (a_0 \cdot a_1) \cdot a_2$ il suffit de prendre la sortie d’une des portes ET et de la câbler sur un autre porte ET en entrée comme ceci :
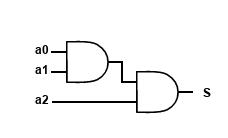
Si on observe bien le schéma on se rend compte que si $a_0 \cdot a_1 = 1 \leftrightarrow a_0 = 1$ et $a_1 = 1$ autrement dit si la sortie du premier ET vaut $1$ alors c’est que le deux premières entrées sont actives, il suffit de voir que $S = 1$ si l’entré $a_2 = 1$ et que la première sortie est allumé, soit que $a_0 \cdot a_1 \cdot a_2 = 1$ ce qui est bien la condition que nous avons fixé. Ensuite pour faire un opérateur à $4$ entrées, le plus simple est de rajouter les entrées d’un opérateur ET (ou porte logique) sur la sortie $S$ et un libre pour constituer $a_3$. Pour $n$ il suffit de mettre $n-1$ portes logiques en série et de laisser à chaque fois une entrées de libre.
Le cours montre donc comment obtenir des portes logiques ET avec des transistors. La suite des cours montrera l’autre porte élémentaire la porte OU : $+$.

